CBSE CLASS 9 MATHS SAMPLE PAPER – 1
CBSE Board
Class IX MATHEMATICS
Sample Paper
Time: 3 hrs. Total marks: 80
General Instructions:
1.All questions are compulsory.
2.The Question Paper consists of 40 questions divided into four sections A, B C and D.
3.Section A contains 20 questions of 1 mark each, Section B contains 6 questions of 2 marks each, Section C contains 8 questions of 3 marks each and Section D contains 6 questions of 4 marks each.
4.There is no overall choice in the paper. However, internal choice is provided in 3 questions of 1 mark, 1 question in 2 marks, 2 questions in 3 marks and 3 questions of 4 marks.
5.Use of calculators is not permitted.
Section-A
Questions 1 to 10 are multiple choice questions. Select the most appropriate answer from the given options.
Q1. The reason that a degree one polynomial equation called a linear equation is that
- It has infinitely many solutions.
- The geometrical representation is a straight line.
- It has two variables.
- Both (a) and (b)
Q2. If the probability of winning a game is , then probability of losing it is
- 6
- 7
- 5
- None of these
Q3.The value of $51^{2}-50^{2}$ is:
- 100
- 101
- 1
- 201
Q4. If two lines intersect each other, then the vertically opposite angles are:
- Equal
- Unequal
- Cannot be determined
- None of the above
Q5. $3 sqrt{2}+sqrt{2}$ is equal to
- $5 sqrt{2}$
- $4 sqrt{2}$
- $2 sqrt{5}$
- $4 sqrt{5}$
Q6. Which point lies on 1st quadrant
- (4,0)
- (0,4)
- (4,4)
- (-4, -4)
Q7. co-ordinate of a point is positive in:
- I and II quadrants
- I and IV quadrants
- I quadrant only
- II quadrant only
Q8. In two triangles, ABC and PQR, ∠A = 30°, ∠B = 75°, ∠P = 75°, ∠Q = 80° and AB = RP, then
- ΔABC ≌ ΔPQR
- ΔABC ≌ ΔQRP
- ΔABC ≌ ΔRPQ
- ΔABC ≌ ΔRQP
Q9. Base of a right triangle is 5 cm and the hypotenuse 6 cm. Its area will be?
- 5 cm2
- 96 cm2
- 24 cm2
- None of these
Q10.The complement of $50^{circ}$ is:
- $40^{circ}$
- $50^{circ}$
- $60^{circ}$
- $90^{circ}$
(Questions 11 to 15) Fill in the Blanks.
Q11. If the height of a triangle is double then its area will become…………………………………………… of the original area.
Q12. The sum of the areas of the plane and curved surfaces (faces) of a solid is called its……… surface area.
Q13. The perpendicular distance of point P (5,4) from X-axis is …………
Q14. If the lengths of two sides of an isosceles triangle are 6 cm and 12 cm, then the length of the third side is……………. cm.
Q15. In ΔABC, AB = AC and Then ∠A is equal to ……….
(Questions 16 to 20) Answer the following:
Q16. The following number of goals were scored by a team in a series of 12 matches: 2, 4, 5, 6, 0, 1, 4, 4, 5, 3, 4, 2 Find the median of these scores.
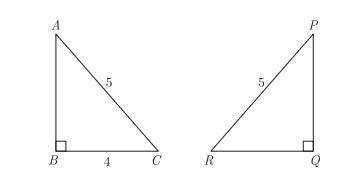
Q17. If ∆ABC is congruent to ∆PQR, find the length of QR.
Q18. Find the mean of the first six multiples of 6.
Q19. Find the height of a cone whose diameter is 10 m and slant height are 6 m.
Q20. Three angles of a quadrilateral measure 50°, 110° and 85°. Find the measure of the fourth angle
Section-B
Q21. Using Heron’s formula, find the area of an equilateral triangle whose perimeter is 123 cm.
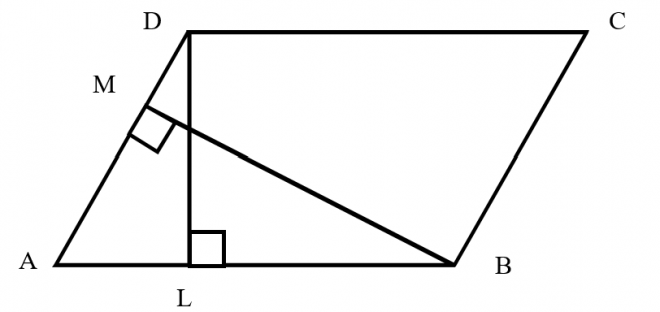
Q22. In the below figure, ABCD is a parallelogram; AB = 12 cm; BM = 6 cm and DL =8 cm, then find AD.
Q23 If a diameter of a circle bisects each of the two chords of a circle, then prove that the chords are parallel.
Q24.In a survey of 200 ladies, it was found that 140 like coffee, while 60 dislike it. Find the probability that a lady chosen at random (i) likes coffee, (ii) dislikes coffee.
Q25. A solid right circular cone or radius 4 cm and height 7 cm is melted to form a sphere. Find the radius of sphere.
Q26.Find the value of $k$ if $(x-1)$ is a factor of $5 x^{3}+4 x^{2}-6 x+k$
Q27. The mean monthly salary of 10 members of a group is Rs. 1500, one more member whose monthly salary is Rs.500 has joined the group. Find the mean monthly salary of 11 members of the group.
Q28. The perimeter of a triangle is 60 cm. One side of a triangle is 5 cm longer than the smaller side and the third side is 8 cm less than twice the smaller side. Find the area of the triangle.
Q29. If the base of an isosceles triangle is produced on both sides, prove that the exterior angles so formed are equal to each other.
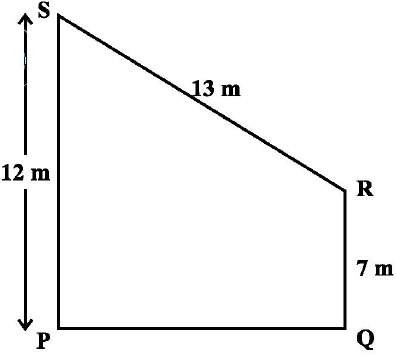
Q30. Find the area of the trapezium PQRS with height PQ given in the Figure.
Q31. Prove that the diagonals of a parallelogram bisect each other.
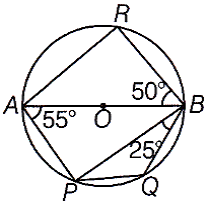
Q32. In the given figure, AB is a diameter of a circle with Centre O. If ∠PAB = 55°, ∠PBQ = 25° and ∠ABR = 50°, then find ∠PBA, ∠BPQ and ∠BAR.
Q33. Find the value of c and d in .
Q34. Two chords AB and CD of lengths 6 cm and 12 cm respectively of a circle are parallel to each other and are on opposite sides of its Centre. If the distance between AB and CD is 6 cm, find the radius of the circle.
Section-D
Q35.In a ΔABC, find the measures of the angles of the triangle formed by joining the mid-points of the sides of the triangle.
Q36. Water is flowing at the rate of 4 km/hour through a circular pipe of 26 cm internal diameter into a circular cistern of diameter 12 m and depth 3 m. In how much time will the cistern be filled?
Q37. Shanti Sweets Stall was placing an order for making cardboard boxes for packing their sweets. Two sizes of boxes were required. The bigger of dimensions 30 cm × 25 cm × 6 cm and the smaller of dimensions 15 cm × 12 cm × 5 cm. For all the overlaps, 5% of the total surface area is required extra. If the cost of the cardboard is Rs 4 for 1500 cm2, find t
he cost of cardboard required for supplying 300 boxes of each kind.
Q38. A solid cylinder has total surface area of 562 sq cm. Its curved surface area is one-third of its total surface area. Find the volume of the cylinder.
Q39. A recent survey found that the age of workers in a factory as follows:
| Age (in yr.) | 20-29 | 30-39 | 40-49 | 50-59 | 60 and above |
| Number of workers | 40 | 25 | 90 | 48 | 4 |
If a person is selected at random, then find the probability that the person is
(i) 40 yr. or more.
(ii) Under 40 yr.
(iii) Having age from 30-39 yr.
Q40. Draw the graph of equation 6x + 4y = 6 and check whether
(a) x = 2, y = 5
(b) x = −1, y = 3 are solutions.