CBSE CLASS 9 MATHS SAMPLE PAPER – 2

Section-A

(Question numbers 1 to 6 carry 1 mark each)

Q. No.

1.

If $mathrm{x}^{mathrm{a} / mathrm{b}}=1$, then find the value of ‘a’.

2.

If $mathrm{p}(mathrm{x})=2 mathrm{x}^{3}+5 mathrm{x}^{2}-3 mathrm{x}-2$ is divided by $mathrm{x}-1$, then find the remainder.

3.

The distance of the point $(0,-1)$ from the origin is

4.

If the vertical angle of an isosceles triangle is $100^{circ}$, then find the measures of its base angles.

5.

The ratio of the whole surface area of a solid sphere and a solid hemisphere is

6.

There are 60 boys and 40 girls in a class. A student is selected at random. Find the probability that student is a girl.

Section B

(Question numbers 7 to 12 carry 2 marks each)

7.

If $p=2-a$, then prove that $a^{3}+6$ a $p+p^{3}-8=0$.

8.

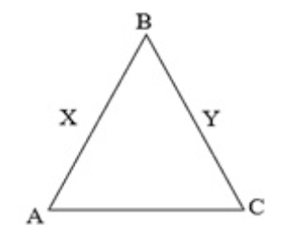
In the adjoining figure, we have $mathrm{AB}=mathrm{BC}, mathrm{BX}=mathrm{BY}$. Show that $mathrm{AX}=mathrm{CY}$ (using appropriate Euclid’s axiom)

9.

If two opposite angles of a parallelogram are $(63-3 x)^{circ}$ and $(4 x-7)^{circ} .$ Find all the angles of the parallelogram.

10.

Three Schools situated at $mathrm{P}, mathrm{Q}$ and $mathrm{R}$ in the figure are equidistant from each other as shown in the figure. Find $angle$ QOR.

11.

The diameter of the two right circular cones are equal if their slant heights are in the

ratio $3: 2$, then what is the ratio of their curved surface areas?

12.

A batsman in his $11^{text {th }}$ innings makes a score of 68 runs and there by increases his average score by 2 . What is his average score after the $11^{text {th }}$ innings.

Section C

(Question numbers 13 to 22 carry 3 marks each)

13.

Represent $sqrt{10}$ on the number line.

14.

Simplify: $frac{73 times 73 times 73+27 times 27 times 27}{73 times 73-73 times 27+27 times 27}$

15.

Determine the point on the graph of the linear equation $2 mathrm{x}+5 mathrm{y}=19$, whose ordinate is $1 frac{1}{2}$ times its abscissa.

16.

Locate the points $(3,0),(-2,3),(2,-3),(-5,4)$ and $(-2,-4)$ in Cartesian plane. Also find the quadrant in which they lie.

OR

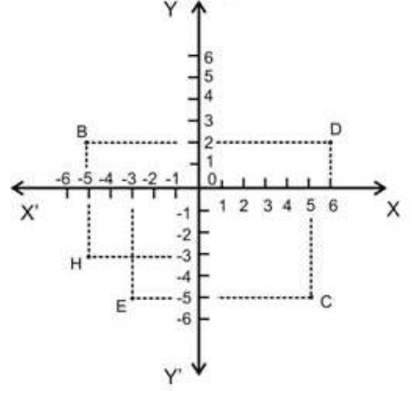
Observe the fig. given below and answer the following:

i.

The coordinates of $mathrm{B}$.

ii.

The coordinates of $mathrm{C}$.

iii.

The point identified by the coordinate $(-3,-5)$.

iv.

The coordinates of $mathrm{H}$.

v.

The coordinates of origin

vi.

The abscissa of the point $mathrm{D}$.

17.

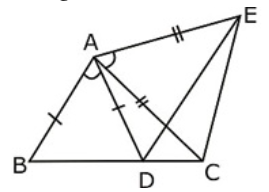
In figure, $A C=A E, A B=A D$ and $angle B A D=angle E A C .$ Show that $B C=D E$.

OR

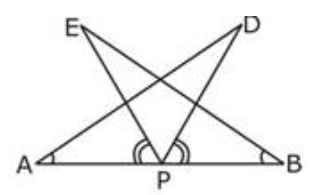
$mathrm{AB}$ is a line segment and $mathrm{P}$ is its mid-point. D and $mathrm{E}$ are points on the same side of $mathrm{AB}$ such that $angle mathrm{BAD}=angle mathrm{ABE}$ and $angle mathrm{EPA}=angle mathrm{DPB}$. Show that:

i.

$triangle mathrm{DAP} cong triangle mathrm{EBP}$

ii.

$mathrm{AD}=mathrm{BE}$

18.

Show that the area of a rhombus is half the product of the lengths of its diagonals.

19.

$mathrm{A}, mathrm{B}, mathrm{C}$ and $mathrm{D}$ are the four points on a circle. AC and BD intersect at point $mathrm{E}$ such that $angle$ $mathrm{BEC}=130^{circ}$ and $angle mathrm{ECD}=20^{circ} .$ Find $angle mathrm{BAC}$.

OR

Prove that equal chords of a circle subtend equal angles at the centre.

20.

Sides of a triangle are in the ratio $12: 17: 25$ and its perimeter is $540 mathrm{~cm}$. Find its area.

21.

The diameter of a garden roller is $14 mathrm{~m}$ and it is $2 mathrm{~m}$ long. How much area will it cover in 10 revolutions?

OR

The sum of height and radius of the base of a solid cylinder is $37 mathrm{~cm}$. If the total surface area of the cylinder is $1628 mathrm{~cm}^{2}$, then find its volume.

22.

Fifty seeds were selected at random from each 5 bags seeds and were kept under standardized conditions favorable to germination. After days, the number of seeds which

had germinated in each collection were counted and recorded as follows:

What is the probability of germination of

i.

More than 40 seeds in a bag

ii.

49 seeds in a bag

iii.

More than 35 seeds in a bag

Section D

(Question numbers 23 to 30 carry 4 marks each)

23.

If $mathrm{x}=frac{6-sqrt{3} 2}{2}$, then find the value of $left(x^{3}+frac{1}{x^{3}}right)-6left(x^{2}+frac{1}{x^{2}}right)+left(x+frac{1}{x}right)$.

OR

If $x=frac{sqrt{3}+1}{sqrt{3}-1}, y=frac{sqrt{3}-1}{sqrt{3}+1}$, find the value of $x^{2}+x y-y^{2}$

24.

Determine the value of $mathrm{b}$ ‘ for which the polynomial $5 mathrm{x}^{3}-mathrm{x}^{2}+4 mathrm{x}+mathrm{b}$ is divisible by $1-5 mathrm{x}$.

25.

Draw the graph of two lines whose equations are $x+y-6=0$ and $x-y-2=0$, on the same graph paper. Find the area of triangle formed by the two lines and y axis.

OR

The force exerted to pull a cart is directly proportional to the acceleration produced in the cart. Express the statement as a linear equation in two variables and draw the graph

for the same by taking the constant mass equal to $6 mathrm{~kg}$.

26.

In figure the sides $A B$ and AC of are produced to points $E$ and D respectively. If bisectors $mathrm{BO}$ and $mathrm{CO}$ of $angle mathrm{CBE}$ and $angle mathrm{BCD}$ respectively meet at point $mathrm{O}$, then prove that $angle mathrm{BOC}=90^{circ}-frac{1}{2} angle mathrm{BAC}$

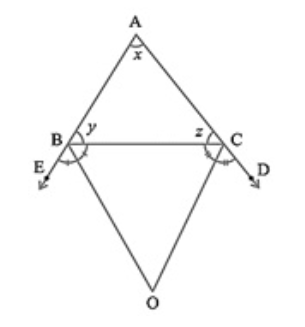
27.

In the adjoining figure, $mathrm{P}$ is the point in the interior of a parallelogram $mathrm{ABCD}$. Show that $operatorname{ar}(triangle mathrm{APB})+operatorname{ar}(triangle mathrm{PCD})=frac{1}{2} operatorname{ar}(|| mathrm{gm} mathrm{ABCD})$

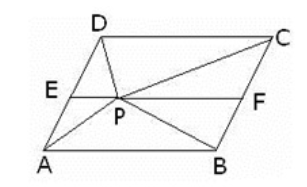
28.

Construct a right angled triangle whose base is $5 mathrm{~cm}$ and sum of its hypotenuse and other side is $8 mathrm{~cm}$.

29.

The floor of a rectangular hall has a perimeter $300 mathrm{~cm}$. Let the cost of painting of four walls at the rate of Rs.12 per $mathrm{cm}^{2}$ is Rs. 24,000 , then find the height of the hall.

30.

The marks obtained (out of 100) by a class of 80 students are given below:

Construct a histogram to represent the data above.

OR

Construct a frequency polygon for the following data: