|
Q. No.
|
Question
|
Marks
|
|
1.
|
|
|
|
a)
|
Show that $sqrt{5}$ is an irrational number
|
3
|
|
b)
|
Express $0.001$ as a fraction in the simplest form.
|
3
|
|
c)
|
Find the median of the following set of numbers:
$7,80,5,81,18,27,4,48,12,47,9,15$
|
4
|
|
2.
|
|
|
|
a)
|
Use congruency of triangles to find the value of x and y.

|
3
|
|
b)
|
Two concentric circles are of radii 7 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
|
3
|
|
c)
|
The compound interest on a certain sum of money at 7% p.a. for 5 years is Rs. 300. Find the sum.
|
4
|
|
3.
|
|
|
|
a)
|
If $frac{sqrt{11}-sqrt{7}}{sqrt{11}+sqrt{7}}=x-y sqrt{77}$, find the values $x$ and $y$.
|
3
|
|
b)
|
Given $log x=mathrm{a}+mathrm{b}$ and $log mathrm{y}=mathrm{a}-mathrm{b}$, find the value of $log frac{10 x}{y^{2}}$ in terms of ‘ $mathrm{a}$ ‘ and ‘ $mathrm{b}$ ‘.
|
3
|
|
c)
|
Sonu and Suraj had adjacent triangular fields with a common boundary of 25 m. The other two sides of Sonu’s field were 52 m and 63 m, while Suraj’s were 114 m and101 m. If the cost of fertilization is Rs 20 per sq m, then find the total cost of fertilization for both of Sonu and Suraj together.
|
4
|
|
4.
|
|
|
|
a)
|
Evaluate $frac{4}{tan ^{2} 60^{circ}}+frac{1}{cos ^{2} 30^{circ}}-tan ^{2} 45^{circ}$
|
3
|
|
b)
|
The bisector of $angle mathrm{A}$ of a $triangle mathrm{ABC}$ meets $mathrm{BC}$ at $mathrm{D}$ and $mathrm{BC}$ is produced to $mathrm{E}$. prove that $angle mathrm{ABC}+angle mathrm{ACE}=2 angle mathrm{ADC}$
|
3
|
|
c)
|
The difference between the exterior angle of a regular polygon of $mathrm{n}$ sides and a regular polygon of $(mathrm{n}+2)$ sides is 6 . Find the number of sides
.
|
4
|
|
SECTION – B (40 Marks)
(Answer any four questions from this Section)
|
|
|
5.
|
|
|
|
a)
|
Graphically solve the simultaneous equations: $x-2 y=1 ; x+y=4$
|
4
|
|
b)
|
How many sides does a regular polygon have, each angle of which is of measure $108^{circ}$ ?
|
3
|
|
c)
|
Prove that the interior angle of a regular pentagon is three times the exterior angle of a regular decagon.
|
3
|
|
6.
|
|
|
|
a)
|
In the given figure, $mathrm{m} angle mathrm{PSR}=90^{circ}, mathrm{PQ}=10 mathrm{~cm}, mathrm{QS}=6 mathrm{~cm}, mathrm{RQ}=9 mathrm{~cm} .$ Calculate the length of PR.
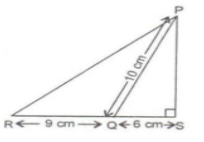
|
3
|
|
b)
|
A and B together can do a piece of work in 15 days. If A’s one day’s work is $frac{3}{2}$ times B’s one day’s work; in how many days can $A$ and $B$ do the work alone?
|
3
|
|
c)
|
Prove that: $9^{log 4}=16^{log 3}$
|
4
|
|
7.
|
|
|
|
a)
|
In the figure, $Q$ is a point on side of $Delta$ PSR such that $P Q=P R$. Prove that $P S>P Q$.
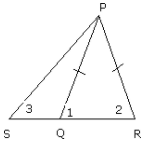
|
4
|
|
b)
|
The amount at compound interest which is calculated yearly on a certain sum of money is Rs. 1250 in one year and Rs. 1375 in two years. Calculate the rate of interest.
|
3
|
|
c)
|
The dimensions of a rectangular field are $120 mathrm{~cm} times 70 mathrm{~cm}$. The field is to be changed into garden, leaving a path way of $5 mathrm{~m}$ width around the garden. Find the expenses that are met when the cost per square meter is Rs. 10 .
|
3
|
|
8.
|
|
|
|
a)
|
In a rectangle PQRS, prove that $mathrm{PR}^{2}+mathrm{QS}^{2}=mathrm{PQ}^{2}+mathrm{QR}^{2}+mathrm{RS}^{2}+mathrm{SP}^{2}$
|
4
|
|
b)
|
Use graph paper for this question:
|
6
|
|
i.
|
Draw the graph of $3 x-y-2=0$ and $2 x+y-8=0 .$ Take $1 mathrm{~cm}=1$ unit on both the axes and plot only three points per line.
|
|
|
ii.
|
Write down the co-ordinates of the point of intersection.
|
|
|
9.
|
|
|
|
a)
|
In a river, a boat covers $8 mathrm{~km}$ in $40 mathrm{~min}$ while travelling $underline{text { downstream, but takes }} 60 mathrm{~min}$ for the return journey. If the speed of the boat and the flow of the river are uniform, find the speed of the boat in still water and speed of the stream.
|
4
|
|
b)
|
A man starts his job with a certain monthly salary and earns a fixed increment every year. If his salary was Rs. 1500 after 4 years of service and Rs. 1800 after 10 years of his service, what was his starting salary and what is the annual increment?
|
3
|
|
c)
|
Solve: $3 p-2 q=5, q-1=3 p$
|
3
|
|
10.
|
|
|
|
a)
|
In the given figure, $A B C D$ is a parallelogram in which $X$ and $Y$ are the midpoints of $A D$ and BC respectively, Prove that: $mathrm{AE}=mathrm{EF}=mathrm{FC}$.
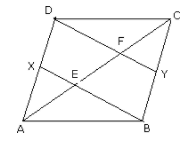
|
4
|
|
b)
|
Two chords $mathrm{AB}$ and CD of lengths $5 mathrm{~cm}$ and $11 mathrm{~cm}$ respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between $A B$ and CD is 6 $mathrm{cm}$, then find the radius of the circle.
|
3
|
|
c)
|
3 equal cubes are placed adjacently in a row. Find the ratio of the total surface area of the new cuboid to that of the sum of the surface areas of three cubes.
|
3
|
|
11.
|
|
|
|
a)
|
In the given figure, area of $Delta mathrm{PQR}=44.8 mathrm{~cm}^{2}, mathrm{PL}=mathrm{LR}$ and $mathrm{QM}=mathrm{MR}$. Find the area of Find the area of DLMR.
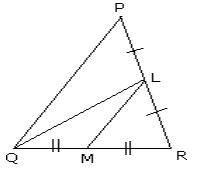
|
4
|
|
b)
|
Factorize: $x^{3}-3 x^{2}-x+3$
|
3
|
|
c)
|
The mean of 5 numbers is $20 .$ If one number is excluded the mean of the remaining numbers becomes $23 .$ Find the excluded number.
|
3
|


